原题:
甲、乙两车分别从A、B 两地同时出发,相向而行,出发时甲、乙两车的速度比是5:4.相遇后甲的速度减少 20%,乙的速度增加 20%,这样当甲到达B地时,乙离A地还有8千米,那么A、B 两地相距多少千米?

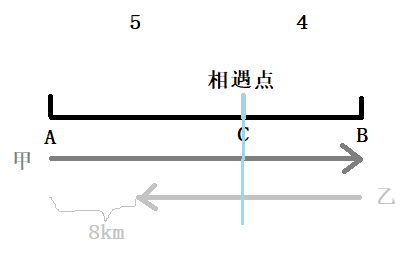
1. 设初始速度与相遇点

设出发时甲速度 $5v$，乙速度 $4v$，A、B 相距 $s$ 千米。

相遇时，两车行驶时间相同 $\Rightarrow$ 路程比 = 速度比 = $5:4$。

所以相遇时甲走了 $\frac{5}{9}s$，乙走了 $\frac{4}{9}s$。

2. 相遇后速度变化

• 相遇后甲速度减少 20%：新速度 = $5v \times (1 - 20$ %$) = 5v \times 0.8 = 4v$

• 相遇后乙速度增加 20%：新速度 = $4v \times (1 + 20$%$) = 4v \times 1.2 = 4.8v$。

3. 相遇后行程分析

相遇后，甲到达 B 地的路程 = 相遇前乙走的路程 = $\frac{4}{9}s$。

相遇后，甲速度 = $4v$，所以相遇后，甲 到 B 的时间：
$t = \frac{\frac{4}{9}s}{4v} = \frac{s}{9v}.$

在这段时间 $t$ 内，乙从相遇点向 A 地行驶的路程 = 乙相遇后速度 × 时间：
$4.8v \times \frac{s}{9v} = \frac{4.8}{9}s = \frac{48}{90}s = \frac{8}{15}s.$

4. 乙离 A 地的距离

相遇时，乙在距 A 地 $\frac{5}{9}s$ 的位置（因为甲从 A 出发走了 $\frac{5}{9}s$ 与乙相遇，所以乙离 A 还有 $\frac{5}{9}s$）。

相遇后，乙向 A 地走了 $\frac{8}{15}s$，所以乙离 A 的距离为：
$\frac{5}{9}s - \frac{8}{15}s.$

通分：$\frac{25}{45}s - \frac{24}{45}s = \frac{1}{45}s$。

已知这个距离是 8 千米：
$\frac{1}{45}s = 8$
$s = 8 \times 45 = 360$

最终答案：

A、B 两地相距 360 千米。

所用的小学数学知识点分析

1. 比例分配

   • 根据速度比 5:4，将总路程 S 按比例分配给相遇时两车的路程。

2. 百分数的应用

   • 速度减少 20% → 乘 0.8；速度增加 20% → 乘 1.2。

3. 行程问题公式

   • 路程 = 速度 × 时间。

4. 分数运算

   • 通分、分数减法：

\frac{5}{9} - \frac{8}{15} = \frac{25}{45} - \frac{24}{45} = \frac{1}{45}

5. 解一元一次方程

   \frac{1}{45} \times S = 8
   解得
   S = 360 。

6. 等时性原理

   • 相遇后甲到 B 的时间 = 乙继续走的时间。

这道题是典型的“变速行程问题”，考查比例、百分数、分数运算与行程结合的能力，是小学高年级竞赛常见题型。