风筝模型（Kite Model）

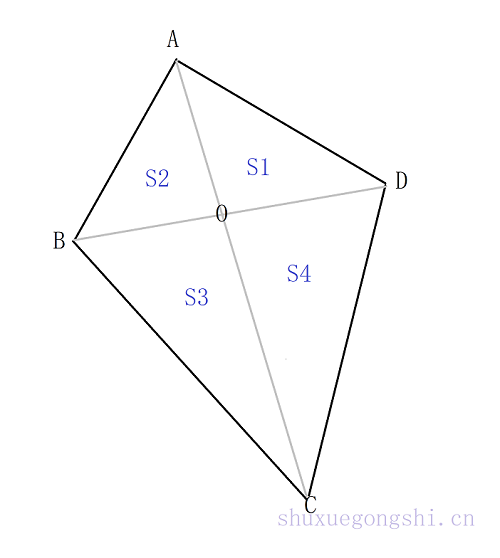
1. 定义：

在一个任意四边形ABCD中，连接对角线AC和BD，它们相交于点O。 这样，四边形被分成了四个部分，其形状像一只风筝（如上图所示）。

该模型研究的是：内部相邻两个三角形之比。
例如:
$\frac{S3}{S2} = \frac{BO}{OD}$
$\frac{S2}{S1} = \frac{AO}{OC}$

$\frac{S2}{S1} = \frac{BO}{OD}$
$\frac{S3}{S4} = \frac{BO}{OD}$
$\Rightarrow$
$\frac{S2}{S1} = \frac{S3}{S4}$
$\Rightarrow$
$\frac{S1}{S2} = \frac{S4}{S3}$
利用：内项积=外项积

$\Rightarrow$

$S1 \times S3 = S4 \times S2$ ★★★

进一步扩展：

• 当上面的任意四边形为平行四边形时， S1=S2, S3=S4
  

  

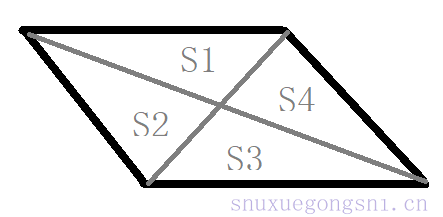
• 当上面的任意四边形为梯形时， S2=S4, S3>S2(S4)>S1
  

  

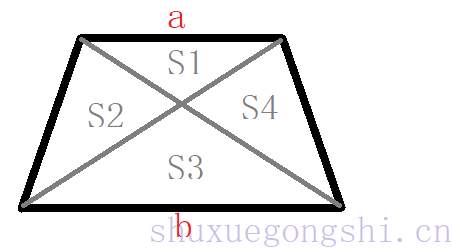
$S1:S2:S3:S4=a^2:ab:b^2:ab$

蝴蝶模型（Butterfly Model）：

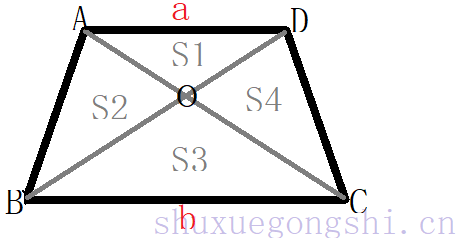
$S1:S2:S3:S4=a^2:ab:b^2:ab$ ★★★

推导过程(了解)

第 1 步：证明 (S_2 = S_4)（左右翅膀面积相等）

考虑 $\triangle ABC$ 与 $\triangle DBC$：
它们有公共底 $BC$；
因为 $AD \parallel BC$，所以它们的高相等（平行线间距离）。
因此：
$S_{\triangle ABC} = S_{\triangle DBC}$
又因为：
$S_{\triangle ABC} = S_2 + S_3, \quad S_{\triangle DBC} = S_3 + S_4,$
两式相减（(S_3) 为公共部分）得：
$S_2 = S_4.$

结论 1：$S_2 = S_4$。

第 2 步：证明 (\triangle AOD \sim \triangle COB) 及面积比

在$\triangle AOD$ 与 $\triangle COB$ 中：
$\angle OAD = \angle OCB$（内错角，$AD \parallel BC$）
$\angle ODA = \angle OBC$（内错角）
$\angle AOD = \angle COB$（对顶角）
所以：
$\triangle AOD \sim \triangle COB.$
相似比：
$\frac{AO}{OC} = \frac{DO}{OB} = \frac{AD}{BC} = \frac{a}{b}.$
面积比：
$\frac{S_1}{S_3} = \left( \frac{a}{b} \right)^2 = \frac{a^2}{b^2}.$
结论 2：$S_1 : S_3 = a^2 : b^2$。

第 3 步：建立 (S_1) 与 (S_2) 的关系（利用等高）

在 $\triangle ABC$ 中，考察 $\triangle AOB$（面积 $S_2$）与 $\triangle COB$（面积 $S_3$）：
它们有公共顶点 $B$，底边 $AO$ 与 $OC$ 在直线 $AC$ 上；
从 $B$ 到 $AC$ 的高相同。
所以面积比等于底边比：
$\frac{S_2}{S_3} = \frac{AO}{OC} = \frac{a}{b}. \quad (1)$

在 $\triangle ADC$ 中，考察 $\triangle AOD$（面积 $S_1$）与 $\triangle COD$（面积 $S_4$）：
它们有公共顶点 $D$，底边 $AO$ 与 $OC$ 在直线 $AC$ 上；
从 $D$ 到 $AC$ 的高相同。
所以：
$\frac{S_1}{S_4} = \frac{AO}{OC} = \frac{a}{b}. \quad (2)$
由 结论 1 (S_4 = S_2)，代入 (2) 得：
$\frac{S_1}{S_2} = \frac{a}{b}. \quad (3)$

第 4 步：统一比例关系

由 (3)：$S_1 : S_2 = a : b$。
由 结论 2：$S_1 : S_3 = a^2 : b^2$。
由 (1)：$S_2 : S_3 = a : b$。
由 结论 1：$S_4 = S_2$，所以 $S_2 : S_4 = 1 : 1$。

设 $S_1 = a^2 k$（$k$ 为比例常数）。
由 $S_1 / S_2 = a / b$ 得 $S_2 = \frac{b}{a} S_1 = \frac{b}{a} \cdot a^2 k = ab k$。
由 $S_1 / S_3 = a^2 / b^2$ 得 $S_3 = \frac{b^2}{a^2} S_1 = \frac{b^2}{a^2} \cdot a^2 k = b^2 k$。
由 $S_4 = S_2 = ab k$。

因此：
$S_1 : S_2 : S_3 : S_4 = a^2 k : ab k : b^2 k : ab k = a^2 : ab : b^2 : ab.$

第 5 步：纠正原图的错误乘积关系

$S_2 \times S_4 = (ab)(ab) = a^2 b^2,$
$S_1 \times S_3 = (a^2)(b^2) = a^2 b^2,$
所以：
$S_1 \times S_3 = S_2 \times S_4.$
这是任意四边形对角线分四块面积都成立的性质，在梯形中自然也成立，并且与本比例一致。

最终结论：
$S1:S2:S3:S4=a^2:ab:b^2:ab$
证明完毕。

内容来源:
https://www.bilibili.com/video/BV16cxUeoE3z