1. 线性相关和线性无关

一组向量 v1⃗,v2⃗,⋯,vn⃗\vec{v_1},\vec{v_2}, \cdots ,\vec{v_n} 是线性相关的

指存在一组不全为零的实数 a1,a2,⋯,ana_1,a_2, \cdots, a_n ，使得：∑i=1naivi⃗=0⃗ \sum^n_{i=1}a_i\vec{v_i} = \vec{0} 。

一组向量 v1⃗,v2⃗,⋯,vn⃗\vec{v_1},\vec{v_2}, \cdots ,\vec{v_n} 是线性无关的，当且仅当ai=0,i=1,2,⋯,n a_i=0, i=1,2,\cdots,n时,才有 ∑i=1naivi⃗=0⃗ \sum^n_{i=1}a_i\vec{v_i} = \vec{0}

2. 维数

一个向量空间所包含的最大线性无关向量的数目，称作该向量空间的维数。

3. 三维向量的点积

假设 u⃗,v⃗\vec{u}, \vec{v} 三维向量分别定义为：

u⃗=(ux,uy,uz)T=[uxuyuz]\vec{u} = (u_x, u_y, u_z)^T = \left[ \begin{array}{ccc} u_x \\\\ u_y \\\\ u_z \end{array} \right]

v⃗=(vx,vy,vz)T=[vxvyvz]\vec{v} = (v_x, v_y, v_z)^T = \left[ \begin{array}{ccc} v_x \\\\ v_y \\\\ v_z \end{array} \right]

那么u⃗,v⃗\vec{u}, \vec{v}的点积为：

u⃗⋅v⃗=uxvx+uyvy+uzvz=∣u⃗∣∣v⃗∣cos(u⃗,v⃗)\vec{u}\cdot\vec{v} = u_xv_x+u_yv_y+u_zv_z = |\vec{u}||\vec{v}|cos(\vec{u},\vec{v})

下图中 u 和 v 是 向量形式：
二、向量操作 - 图1

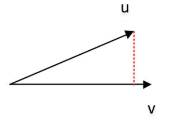
4. 三维向量的叉积

假设 u⃗,v⃗\vec{u}, \vec{v} 三维向量分别定义为：

u⃗=(ux,uy,uz)T=[uxuyuz]\vec{u} = (u_x, u_y, u_z)^T = \left[ \begin{array}{ccc} u_x \\\\ u_y \\\\ u_z \end{array} \right]

v⃗=(vx,vy,vz)T=[vxvyvz]\vec{v} = (v_x, v_y, v_z)^T = \left[ \begin{array}{ccc} v_x \\\\ v_y \\\\ v_z \end{array} \right]

那么u⃗,v⃗\vec{u}, \vec{v}的叉积为：

w⃗=u⃗×v⃗=[i⃗j⃗k⃗uxuyuzvxvyvz]\vec{w} = \vec{u} \times \vec{v} = \left[ \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\\\ u_x & u_y & u_z \\\\ v_x & v_y & v_z \end{array} \right]

其中 i⃗,j⃗,k⃗\vec{i},\vec{j},\vec{k} 分别为 x,y,zx,y,z轴的单位向量。
u⃗=uxi⃗+uyj⃗+uzk⃗ \vec{u} = u_x\vec{i} + u_y\vec{j} + u_z\vec{k}
v⃗=vxi⃗+vyj⃗+vzk⃗ \vec{v} = v_x\vec{i} + v_y\vec{j} + v_z\vec{k}

注：
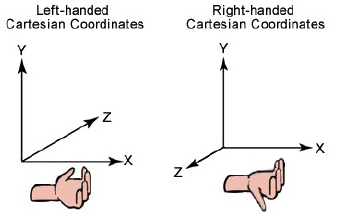
u⃗\vec{u} 和 v⃗\vec{v}的叉积垂直于 u⃗,v⃗ \vec{u}, \vec{v} 构成的平面，其方向符合右手规则。
叉积的模等于 u⃗,v⃗\vec{u},\vec{v}构成的平行四边形的面积。
u⃗×v⃗=−v⃗×u⃗\vec{u}\times\vec{v} = - \vec{v}\times\vec{u}
u⃗×(v⃗×w⃗)=(u⃗⋅w⃗)v⃗−(u⃗⋅v⃗)w⃗\vec{u}\times(\vec{v}\times\vec{w})=(\vec{u}\cdot\vec{w})\vec{v}-(\vec{u}\cdot\vec{v})\vec{w}

二、向量操作 - 图2

shuxuegongshi.cn note：
无论上面的点积还是叉积，只是一种叫法，本质是不同的算法，为了区分这两种不同的算法而起了两个不同的名字。你可以命名为狗积，猫积。无论叫什么名字，只要你能给自己的算法对上号即可。

5. 三维向量的混合积

[u⃗v⃗w⃗]=(u⃗×v⃗)⋅w⃗=u⃗⋅(v⃗×w⃗)=∣uxuyuzvxvyvzwxwywz∣=∣uxvxwxuyvywyuzvzwz∣[\vec{u} \quad \vec{v} \quad \vec{w}] = (\vec{u} \times \vec{v}) \cdot \vec{w} = \vec{u}\cdot (\vec{v}\times\vec{w}) = \left| \begin{array}{ccc} u_x & u_y & u_z \\\\ v_x & v_y & v_z \\\\ w_x & w_y & w_z \end{array} \right| = \left| \begin{array}{ccc} u_x & v_x & w_x \\\\ u_y & v_y & w_y \\\\ u_z & v_z & w_z \end{array} \right|

其物理意义为：以 u⃗,v⃗,w⃗\vec{u},\vec{v},\vec{w} 为三个棱边所围成的平行六面体的体积。
当u⃗,v⃗,w⃗ \vec{u},\vec{v},\vec{w} 构成右手系时，该平行六面体的体积为正号。

6. 两个向量的并矢

给定两个向量 x⃗=(x1,x2,⋯,xn)T,y⃗=(y1,y2,⋯,ym)T\vec{x}=(x_1,x_2,\cdots,x_n)^T ,\vec{y}=(y_1,y_2,\cdots,y_m)^T ，则向量的并矢记作：

x⃗y⃗=[x1y1x1y2⋯x1ymx2y1x2y2⋯x2ym⋮⋮⋱⋮xny1xny2⋯xnym]\vec{x}\vec{y}= \left[ \begin{array}{ccc} x_1y_1 & x_1y_2 & \cdots & x_1y_m \\\\ x_2y_1 & x_2y_2 & \cdots & x_2y_m \\\\ \vdots & \vdots & \ddots & \vdots \\\\ x_ny_1 & x_ny_2 & \cdots & x_ny_m \end{array} \right]

也记作 x⃗⊗y⃗\vec{x} \otimes \vec{y} 或者 x⃗y⃗T \vec{x}\vec{y}^T