排列

由于 $det(a_1,a_2,\cdots,a_n)$ 中任意两个向量的位置发生变化后要变号，因此其符号与向量的排序有关，因此在此提出排列的概念。

排列：把从1到N的n个自然数 $i_1,i_2, \cdots , i_n$，按任意顺序排成一行。

例如：
将1到5排列成$(2,1,4,3,5)$ 。

标准排列：从小到大排列。

例如：
($i_1 < i_2 < \cdots < i_n$)

逆序：如果排列中有两个数 $i_m,i_n$，且$i_m > i_n$，那么这个排列$(i_m,i_n)$就算一个逆序。

注：
白话:从大到小数的所有组合数。

例如：
$(1,3,2)$中有1个逆序:$(3,2)$
$(3,1,2)$中有2个逆序:$(3,1)$、$(3,2)$
$(3,2,1)$中有3个逆序:$(3,2)$、$(3,1)$、$(2,1)$
将来程序中可能会用到的算法：
一个排序中有几个逆序，其实就是计算机算法中的“冒泡法”恢复标准排列的步骤数。
例如：排列$(4,2,3,1)$中$(4,2)(4,3)(4,1)(2,1)(3,1)$共有5个逆序，而通过“冒泡法”恢复标准排列的步骤数也是5步。

逆序数($\tau$)：一个排列$(i_1,i_2,\cdots,i_n)$中的逆序的个数。记作$\tau(i_1,i_2,\cdots,i_n)$。

技巧：
要数一个排列中的逆序数的方法：(下面2个方法选择1个即可)★★★
方法1：只需从左向右，数每一个数字右边比其小的数字的个数，然后汇总即可。
换句话说： 从左向右看，每一个数字左边比其大的数字的个数。
原则：从左向右看，左大右小。
方法2：反过来，从右向左数每一个数字左边比其小的数字的个数也是一样的。
换句话说： 从右向左看，每一个数字右边比其大的数字的个数。
原则：从右向左看，左小右大。
例如：
$\tau(635412)=5+2+3+2+0=12$
即：
6的右边比6小的数字有5个，
3的右边比3小的数字有2个，
5的右边比5小的数字有3个，
4的右边比4小的数字有2个，
1的右边比1小的数字有0个。

奇排列：逆序数($\tau$)为奇数的排列。
偶排列：逆序数($\tau$)为偶数的排列。

注:
排列的奇偶性：指 奇排列、偶排列。

对换：将一个排列中的两个元素对调位置，其余的元素不动，这种做出新排列的动作称为一次对换。

注：
这两个数可能相邻，也可能不相邻。
相邻对换：相邻两个元素对换。

定理1：对换对奇偶性的改变

解释：
任意一个排列每经过一次对换，则该排列的奇偶性就会发生一次改变。

说明：
(1) 相邻两个数对换，逆序的个数显然要增加1个或减少1个，排列的奇偶性发生1次改变。
例如：$(6,3,5,4,1,2)$中$3,5$交换位置，那么逆序增加一个$(5,3)$；
(2) 不相邻的两个数 对换转化为 多次相邻对换。
白话: 这句话的意思是，对于不相邻的两个数，可以通过多次相邻对换来实现它们的位置交换。
在线性代数中，这可以理解为矩阵中两个元素的位置交换，通过多次对换相邻元素的操作来实现。
假设：(该假设的目的：为了让 $i_p,i_q$ 位置对换)
这两个数分别为$i_p,i_q$，并且设它们之间相隔k个数，那么可以让$i_p$和右边相邻的数依次对换位置，直到与$i_q$相邻，这个过程中共发生了k次对换。
然后再让$i_q$和左边相邻的数依次对换位置，直到进入$i_p$原来的位置，这个过程中将发生k+1次对换。
整个过程共计2k+1次相邻对换，排列的奇偶性必然发生改变。

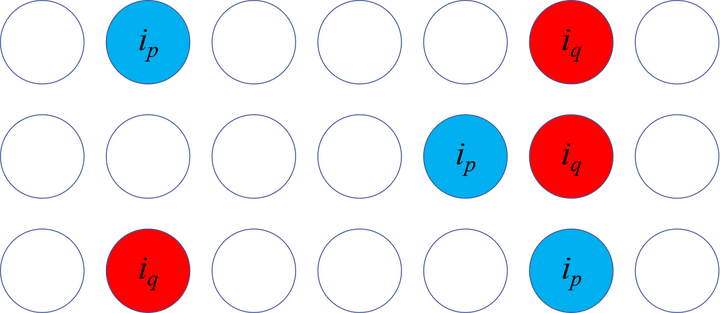
对换次数的奇偶性 定义：
对换次数的奇偶性是指在对一个初始排列进行一系列对换操作后，所需的对换次数是奇数还是偶数。

对换次数：
对换次数用字母s表示。

定理2：对换次数的奇偶性
(1) 任意一个排列都可以经过有限次对换变成标准排列。
(2) 任意一个排列变成标准排列经历的对换次数s可能不唯一，但对换次数s的奇偶性与排列的奇偶性相同。

第(20)条的白话：
这句话涉及到排列论和线性代数中的概念。在线性代数中，排列的奇偶性与对换次数之间存在着关系。一个排列的奇偶性是指该排列所需的对换次数的奇偶性。因此，这句话在线性代数中是正确的。

说明：
(1) 数学归纳法。
n=1时，显然。
假设已经验证命题对于已知的n元排列成立。
那么，对于n+1元排列 $(i_1,i_2,\cdots,i_n,i_{n+1})$，如果$i_{n+1}\neq n+1$，那么前面必有一个元素$i_k=n+1$。将它们俩对换后就能得到新的排列$(i_1,i_2,\cdots,i_n,n+1)$，而新排列的前n元是可以通过有限次对换到标准排列的。总的次数依然是有限次。
(2) 不唯一：
要将排列$(4,2,3,1)$变为标准排列，将4和1对换，$s=1$，也可以依次将4、2，4、3，4、1对换，得到$(2,3,1,4)$ ，在此基础上再将1、3，1、2依次兑换，$s=3+2=5$ 。
奇偶性：
(1) 标准排列的逆序数为0，是偶排列；
(2) 定理1：每一次对换都会改变排列的奇偶性。所以，如果一个排列是偶排列，那么它变成标准排列必须经过偶数次对换；反之，如果它是奇排列，那么它变成标准排列必须经过奇数次对换。
因此有：
(1) $(-1)^{\tau} = (-1)^{s}$
(2) $det(e_{i_1},e_{i_2},\cdots,e_{i_n})=(-1)^{\tau(i_1,i_2,\cdots,i_n)}$。

行列式

A矩阵的行列式（determinant），用符号 det(A) 表示。

determinant
美[dɪˈtɜrmɪnənt]
n: 决定因素；决定条件
adj: 决定性的
网络: 行列式；决定性因素；行列式值

定义

一个排列中的任意两个元素对换，排列的奇偶性会改变。

举例：

一个排列： $(1234)$
按照上面逆序数的方法2可以知道：
$\tau(1234)=0+1+2+3=6$ //属于 偶排列
即：//从右往左看
4的左边比4小的数字有3个，
3的左边比3小的数字有2个，
2的左边比2小的数字有1个，
1的左边比1小的数字有0个。
假设 对换2和4的位置，那么排列变为:
$(1432)$
此时逆序数：
$\tau(1432)=0+1+1+1=3$ //属于 奇排列

$D=2\sqrt{\frac{I}{J\times \pi}}$