如何理解模糊控制中的 三角隶属度 ？

模糊控制是一种基于模糊逻辑的控制方法，通常用于处理不确定性和模糊性问题。在模糊控制中，三角隶属度是一种常见的隶属函数，用于描述模糊集合中元素的隶属度。

理解三角隶属度

三角隶属度函数是一种简单而直观的隶属度函数，它的形状像一个三角形。形状如下图所示：

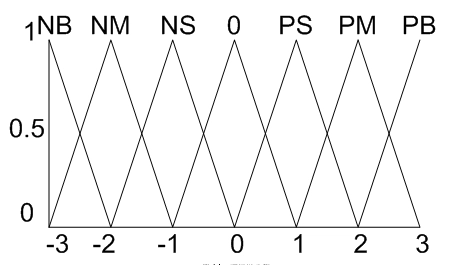
其定义通常包括三个参数：左端点 (a)、顶点 (b) 和右端点 (c)。具体的定义如下：

若 $x < a$，则 $\mu(x) = 0$ 。
若 $a \leq x < b$，则 $\mu(x) = \frac{x - a}{b - a}$。
若 $b \leq x < c$，则 $\mu(x) = \frac{c - x}{c - b}$.
若 $x \geq c$，则 $\mu(x) = 0$。

隶属度的含义

隶属度 $\mu(x)$ 表示输入值 $x$ 属于某个模糊集合（例如“低”、“中”、“高”）的程度，取值范围从 0 到 1。
当 $x$ 等于顶点 $b$ 时，隶属度达到最大值 1，表示 $x$ 完全属于该模糊集合。
在 $a$ 和 $c$ 之间，隶属度线性增长或减少，表示 $x$ 对模糊集合的隶属程度逐渐增强或减弱。

应用举例

举个简单的例子，假设我们在设计一个温度控制系统，其中“温暖”可以用三角隶属度描述：

$a = 15^\circ C$（温暖的最低边界）
$b = 25^\circ C$（温暖的理想值）
$c = 35^\circ C$（温暖的最高边界）

那么，对于某个温度值 $x$，我们可以计算出它对“温暖”这一模糊集合的隶属度。这使得我们能够进行模糊推理，根据隶属度来调整控制策略。

优势

• 简单而直观：三角隶属度函数的定义和计算相对简单，便于理解和实现。
• 灵活性：可以通过调整 ( a )、( b ) 和 ( c ) 参数来灵活地适应不同的应用场景和需求。

总结

三角隶属度在模糊控制中提供了一种有效的方式，使得模糊集合能够具体化，并且通过计算隶属度为控制决策提供依据。它的简单性和直观性使得它在激增模糊控制系统设计中的广泛应用具有吸引力。