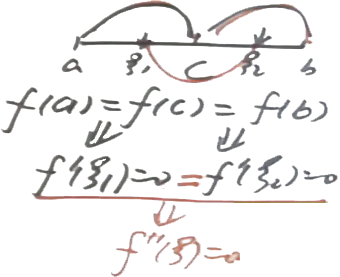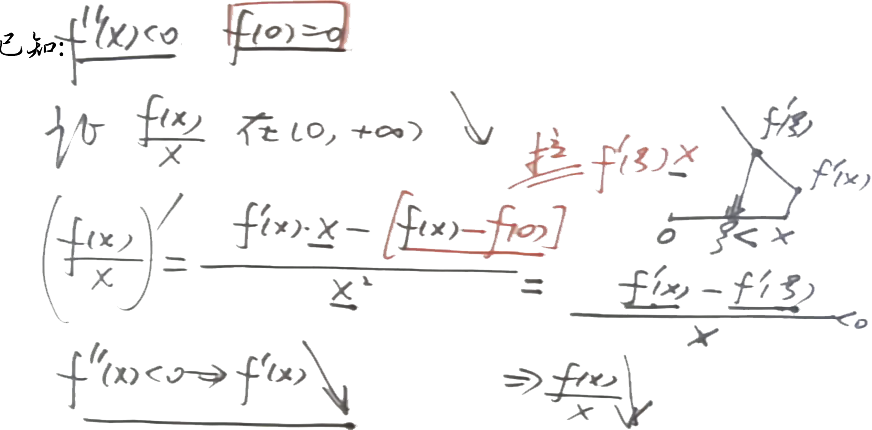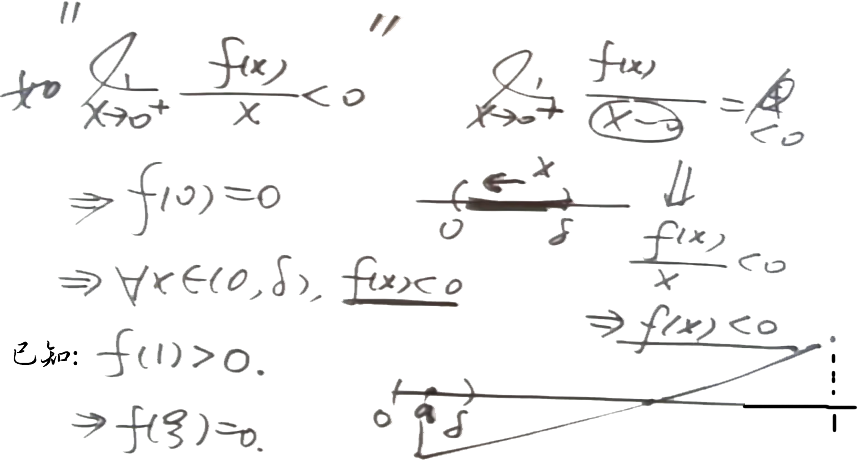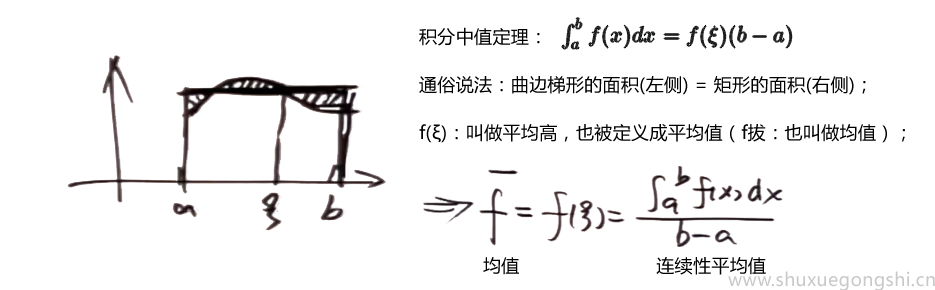一、确定区间
在数轴上标出所有可能用到的点,从而确定区间。
E.g :

二、确定研究对象(辅助函数)
1、简单情形
题设f(x)即为辅助函数。
2、复杂情形
(1) 乘积求导公式逆用;
(u⋅v)′=u′v+uv′⇔u′v+uv′=(u⋅v)′
举例:
①[f(x)⋅f(x)]′=f′(x)f(x)+f(x)f′(x)=2f(x)f′(x)
或
[f2(x)]′=2f(x)⋅f′(x)
记: 见到f(x)⋅f′(x)⇒ 令F(x)=f2(x)
E.g (2017’) 若f(x)⋅f′(x)>0⇒[f2(x)]′>0⇒f2(x)↗⇒1>−1时,f2(1)>f2(−1)
⇒∣f(1)∣>∣f(−1)∣
②[f(x)⋅f′(x)]′=[f′(x)]2+f(x)f′′(x)
记:见到(f′)2+f⋅f′′⇒ 令 F(x)=f(x)⋅f′(x)
③[f(x)⋅eφ(x)]′=f′(x)eφ(x)+f(x)eφ(x)⋅φ′(x)=eφ(x)[f′(x)+f(x)⋅φ′(x)]
注意:如果题目带入ξ,是上面的式子=0,那么你会发现eφ(x)是指数函数,那么它恒>0,所以只有f′(x)+f(x)⋅φ′(x)=0.
记:见到f′+f⋅φ′⇒, 令 F(x)=f(x)eφ(x)
E.g:
A. 见到”f′(x)+f(x)” ⇒ 令F(x)=f(x)⋅ex
例:f′+f⋅1
B. 见到”f′(x)−f(x)” ⇒ 令F(x)=f(x)⋅e−x
例:f′+f⋅(−1)
C. 见到”f′(x)+(21−1)f(x)” ⇒ 令F(x)=f(x)⋅elnx−x
D. 见到”f′(x)+2f(x)” ⇒ 令F(x)=f(x)⋅e2x
E. 见到”f′(x)+f′′(x)tanx”⇒ 令 F(x)=f′(x)⋅sinx
④ (uv)′′=uv′′+2u′v′+u′′v
E.g f′′(ξ)g(ξ)+2f′(x)g′(x)+f(ξ)g′(x)=0
那么我们令F(x)=f(x)⋅g(x)
(2) 商的求导公式逆用
(vu)′=v2u′v−uv′
E.g f(2)−2f(1)=ξf′(x)−f(ξ)
分析后可知,令F(x)=xf(x)+xf(2)−2f(1)
题型:
① (xf(x))′=x2f′(x)⋅x−f(x)
E.g 假如:若x>0,f′(x)⋅x>f(x). 那么可以知道:⇒xf(x)↗⇒b>a,bf(b)>af(a)⇒af(b)>bf(a)
② [lnf(x)]′′=(f(x)f′(x))′=f(x)2f′′(x)f(x)−[f′(x)]2
E.g 假如:f(x)>0,f(x)f′′(x)−[f′(x)]2⩾0, 证明:f(x1)f(x2)⩾f2(2x1+x2)
解: 令F(x)=lnf(x)
(3) 原函数定义 ★
见到∫abf(x)dx=A,令F(x)=∫axf(t)dt,则F(b)=A
即:见到定积分,最好能想到变上限积分;
E.g [68:43]
若f(x)连续,∫−11f(x)dx=∫−11f(x)tanxdx=0,证明:(−1,1)内存在两个不同的ξ1,ξ2,使f(ξ1)=f(ξ2)=0
解:令F(x)=∫−1xf(t)dt,那么F(−1)=0,F(1)=0.
F′(x)=f(x)
dxdF(x)=f(x)
dF(x)=f(x)dx
⇒∫−11tanxdF(x)=tanxF(x)∣−11−∫−11F(x)sec2xdx
设F(x)在(-1,1)内再无零点,且大于0 ⇒∃x0∈(−1,1),使F(x0)=0.
3、更复杂时,题设给出F(x)或F(a),亦可作为提示,让考生令F(x)为辅助函数
E.g
∫0k1xe1−xf(x)dx⇒F(x)=xe1−xf(x)
∫abcos2xf(x)dx⇒F(x)=cos2xf(x)
f2(0)+[f′(0)]2=4⇒F(x)=f2(x)+[f′(x)]2
三、确定定理
Note: 主要用4个,其余用来辅助找点;
1、零点、介值定理
常用来“找”下面的点:
f(c)=0,(f(a)>0,f(b)<0)
f(c)=μ, ①(m⩽μ⩽M) 或②(f(a)=A,f(b)=B.A<μ<B)
2、费马定理
常用于证明f′(ξ)=0,ξ一般是可导点或极值点(内部的最值点);
3、罗尔定理
常用于:
1)证明f′(ξ)=0,(f(a)=f(b))
2)证明fn(ξ)=0,n⩾2 //即:通过画笑脸的方法来证明高阶导数=0;
下图为通过”笑脸”证明2阶导数的过程:
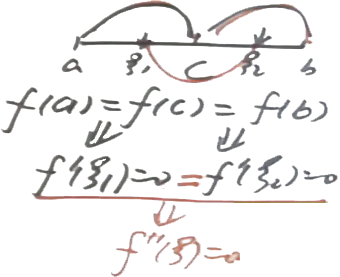
4、拉格朗日
f(b)−f(a)=f′(ξ)(b−a),其中a,b为常数.
往往考试时为:
f(x)−f(x0)=f′(ξ)(x−x0)
来源:
N-L公式:
∫abf(x)dx=F(b)−F(a)
∫abf′(x)dx=f(b)−f(a)
常用于:
(1)题设中有f,f′的关系 或 f−f的关系;
E.g
假如:Un=f(n),问U2和U1的关系?
分析:U2=f(2),U1=f(1),那么U2−U1=f(2)−f(1)=f′(ξ)⋅(2−1)=f′(ξ),
即最后看导数f′(ξ)大小即可.
(2)证f′(ξ)>0 或 f′(ξ)<0; //证相等用罗尔,证不等用拉格朗日;
E.g 1
已知:f(b)=f(a)
证明:f′(ξ)=0
分析:因为f(b)=f(a),所以由罗尔定理可以知道:f′(ξ)=0;
E.g 2
已知:f(b)>f(a),b>a
证明:f′(ξ)>0
分析:因为不等,所以由拉格朗日定理可知f′(ξ)=b−af(b)−f(a)>0
(3)证f(n)(ξ)>0 或 f(n)(ξ)<0 n⩾2;
E.g 1
已知:f(a)=f(b)=f(c)
证明:f′′(ξ)=0
分析:关系如下图所示:

E.g 2
已知:f(a)<f(b)<f(c)
证明:
分析:在(a,b)内任取一点ξ1,那么f′(ξ1)=b−af(b)−f(a)>0;//第1次拉格朗日
在(b,c)内任取一点ξ2,那么f′(ξ2)=c−bf(c)−f(b)<0;//第2次拉格朗日
在(ξ1,ξ2)内任取一点ξ,那么f′(ξ)=ξ2−ξ1f(ξ2)−f(ξ1)<0;//第3次拉格朗日
关系如下图所示:

(4)证 F(f′(ξ),f′(τ))=0
E.g <高数十八讲>
5、泰勒公式
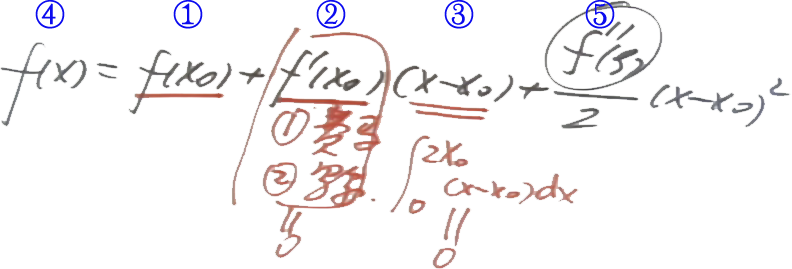
(1)题设中有f与f(n)的关系;n⩾2
思路:把①②③搞成0,然后通过④和⑤的关系即可知上面的关系了;
(2)证明f(n)(ξ)=0
思路:证明①②③④都等于0;
四、确定点的信息
1、用题设告知
例如 1: f(a)=0 //它隐身了,我看到了吗?答:没看到,复习到2点。
E.g
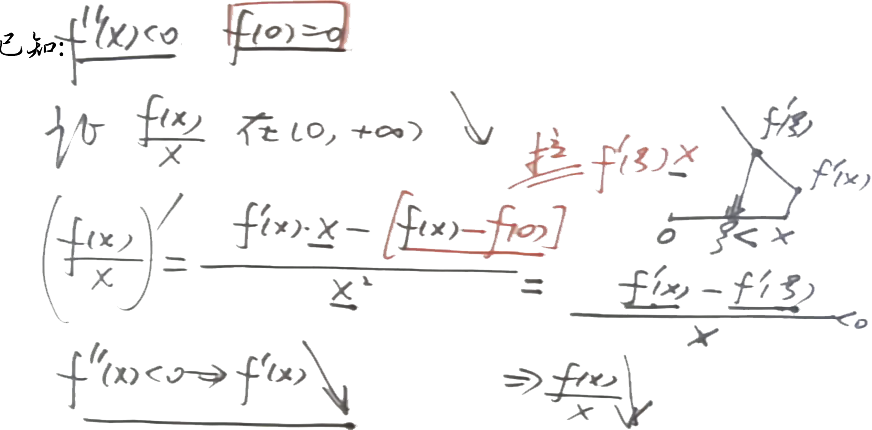
例如 2: f′′(x)>0⇒f′′(ξ)>0;//由一般推出特殊,即知道了⑤;
2、用极限(连续、可导)的条件
(1) 连续的定义
f(x0)=limx→x0f(x)
(2) 可导的定义
f′(x0)=limx→x0x−x0f(x)−f(x0)
(3) 极限的保号性
limx→x0x−x0f(x)−f(x0)>0⇒f′(x0)>0
limx→x0f(x)>0⇒f(x0)>0
(4) 算极限

E.g
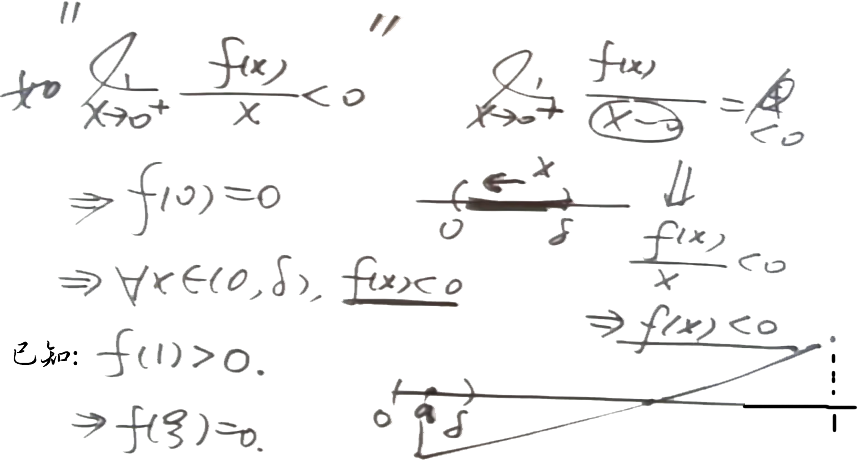
3、用积分确定点的信息
∫abf(x)dx=A
(1)均值定义 ★
指:积分中值定理 ∫abf(x)dx=f(ξ)(b−a),其中ξ既可以取闭区间,也可以取开区间(ξ∈[a,b]orξ∈(a,b)均可直接使用,无需证明);
理解积分中值定理的含义:
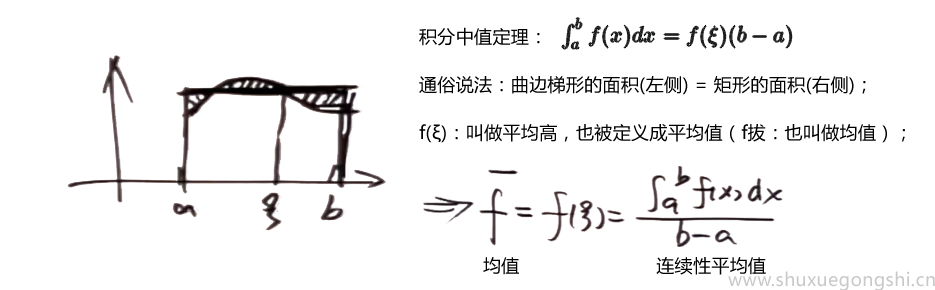
结论:
⇒f=f(ξ)=b−aA
通过该结论也可以确定出点ξ的值f(ξ).
(2) 原函数定义 ★
令F(x)=∫axf(t)dt,则F(a)=0,F(b)=A
E.g
已知:f(x)连续,且∫−11f(x)dx=∫−11f(x)tanxdx=0;
证明:f(ξ1)=f(ξ2)=0,ξ1≠ξ2;
分析:令F(x)=∫−1xf(t)dt,则可知:F(−1)=0(根据我的定义,实际为从-1到-1,肯定积分为0了),F(1)=0(本例的已知条件),所以确定了两点F(−1)=F(1);
(3) 保号性
f(x)在[a,b]上为非负(⩾0)连续且不恒为0⇒∫abf(x)dx>0.
E.g 1:
<高数18讲> P135. E.g7.8
E.g 2: //2019
已知: f(0)=0,f(1)=1,f(x)连续且二阶可导;∫01f(x)dx=1;
证明: ∃ξ∈(0,1),使f′(ξ)=0;
分析: ∫01f(x)dx=1⇒∫01f(x)dx−1=0⇒∫01[f(x)−1]dx=0 //目的:如果要利用保号性,那么就要和0比大小;
假设f(x)⩽1⇒f(x)−1⩽0,且不恒为0. ⇒∫01[f(x)−1]dx<0矛盾,⇒∃x0,使f(x0)>1.根据费马定理可知:f′(ξ)=0.
保号(白话:在区间内,始终保持>0或始终保持<0 ):
1、F(x)在(-1,1)内再无零点,那么F(x)>0或F(x)<0(因为如果在区间内有正有负,那么一定会出现零点);

2、不保号(白话:在区间内不始终保持>0或始终<0),如果在(-1,1)内有零点,那么在区间内F(x)肯定有正有负;
(4) 算积分
<十八讲> E.g 5.4
已知:f(x)在[-a,a]上二阶导连续,f(0)=0⇒m⩽f′′(x)⩽M;
证明:m⩽a33∫−aaf(x)dx⩽M
分析:根据泰勒公式,f(x)=f(0)+f′(0)x+2f′′(ξ)x2,因为已知f(0)=0,所以等式两边同时取积分:
∫−aaf(x)dx=∫−aaf′(0)xdx+∫−aa2f′′(ξ)x2dx
注意:∫−aaxdx=0,∫02(x−1)dx=0,∫04(x−2)dx=0
因为m⩽f′′(x)⩽M⇒m⩽f′′(ξ)⩽M⇒2m⩽2f′′(ξ)⩽2M,根据上面分析可知同时积分:3a3m=2m∫−aax2dx⩽∫−aa2f′′(ξ)x2dx⩽2M∫−aax2dx=3a3M
(5) 用奇偶性质
f(x)奇⇒f(0)=0⇒f′(x)偶⇒f′(x0)=f′(−x0)
E.g (2013)
已知:假设f(x)奇函数,在[−1,1]上二阶可导,f(−1)=1;
证明:∃η∈(−1,1),f′′(η)+f′(η)=1;
分析:1)确定点的信息: 因为f(x)是奇函数,所以f(0)=0.

2)令F(x)=f′(x)+f(x)−x
3)因为f(x)是奇函数,⇒f′(x)偶⇒f′(1)=f′(−1),所以f(−1)=−f(1)=−1.F(−1)=f′(−1)+f(−1)+1=f′(−1),F(1)=f′(1)+f(1)−1=f′(1),根据罗尔定理可知.
(6) 用几何条件
1) f(x)与g(x)存在相等的最大值,即f(a)=g(b)(假设:a为f(x)的取最大值的点,b为g(x)的取最大值的点);
E.g <十八讲>E.g 5.9
1° a=b⇒f(a)=g(a) //即:在相同的点,取到相同的最大值.
E.g 令F(x)=f(x)−g(x)⇒F(a)=0.
2° a≠b⇒F(a)=f(a)−g(a)>0,F(b)=f(b)−g(b)<0,根据零点定理⇒∃c∈(a,b),F(c)=0
2) f(x)与g(x)交于点a⇒f(a)=g(a)⇒F(a)=f(a)−g(a)=0;
E.g <十八讲>E.g 5.10
3) f(x)与g(x)在点a有公切线 ⇒f′(a)=g′(a)⇒F′(a)=f′(a)−g′(a)=0
(7) 用行列式
f(x)=∣∣∣∣∣∣123x2x3x479∣∣∣∣∣∣
⇒f(0)=0,f(1)=0⇒f′(ξ)=0
来源:
https://www.yizhibo.com/l/Kv2NzbQ4ZyPMrpUb.html
https://www.yizhibo.com/l/BSMb91f9PH-QT0DF.html