定义
提出者:

① [a,b]区间内,n等分(n→∞) ⇒每份的底为nb−a;

原文是说在[a,b]内无限切分,但是为了方便考试,所以我们只考虑无穷等分的情况;
② 一般取划分的每块的右端点的高 ⇒每份的高为f(a+nb−a⋅i);
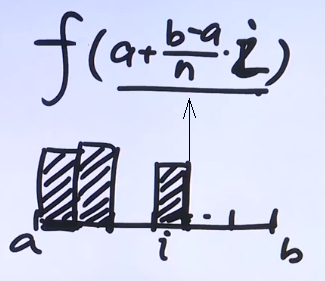
小结:
1、每份的长和宽:
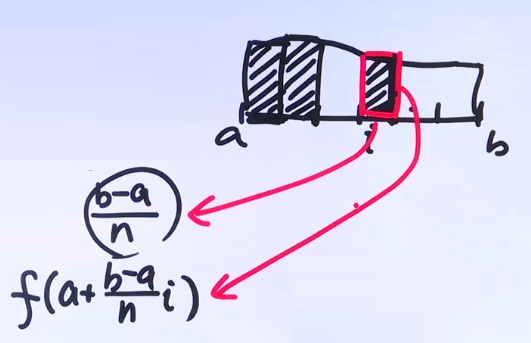
2、limn→∞∑i=1n[f(a+nb−a⋅i)⋅nb−a]=∫abf(x)dx
常见考题的形式:
2.1、基本形(a=0,b=1)
limn→∞∑i=1n[f(0+n1−0⋅i)⋅n1−0]=∫01f(x)dx
⇒ 记住该形式:limn→∞∑i=1n[f(ni)⋅n1]=∫01f(x)dx
上面的公式即:f(ni)→f(x)⇒ni→x , n1→dx
所以要凑出上面的ni,要保证n和i的次数相同!!!
2.1、变量形(a=0,b=x)
⇒ 记住该形式:limn→∞∑i=1n[f(nx⋅i)⋅nx]=∫0xf(t)dt
3、基本形
3.1、能直接凑出ni的形式
① n+i
② n2+i2
③ n2+ni
④ ni
3.2 如果凑不成ni,则直接使用放缩法;
① 直接利用夹逼准则;
② 或放缩后再凑ni;




